
Electric
current









Electric current is a flow of electricity through a medium and its SI unit is the ampere, with the
symbol A. The flow is typically through a wire and composed of electrons, the tiny particles
that make up electricity. For most practical purposes the ampere is a measure of the amount
of electric charge passing a particular point in a given time. To illustrate the ampere we can
ask the simple question: how many electrons does it take to make a cup of tea?
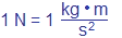

How many electrons are needed to make a cup of tea?

The next SI Unit is the metre (m). Find out how long it would take to walk around planet
Earth. Other SI units are available from the menus at the top of the page.


We more often than not refer to amperes simply as amps, and one amp has the units of 1
coulomb per second. Mathematically we can show this as 1 A = 1 C/s. But what is a
coulomb? It is the derived SI unit of electric charge and 1 coulomb contains around 6.241 x
10
18
electrons. Let's look at that number written out fully:
624,100,000,000,000,000
Remember that this is the amount of electrons passing a single point in a wire every single
second. There are so many of them that it's natural to assume that they are whizzing past at
some tremendous speed, but that's not the case. In fact, they are moving very slowly -
typically only about a metre or two an hour, but they are very, very small.
So we know that 1 A = 1 C/s and we know how many electrons there are in a coulomb. A
typical kettle will draw about 2000 watts of power, and how many coulombs per second that
is depends on the voltage being used. In England, a country associated with drinking
copious amounts of tea, the mains voltage is 230v so we will use that as our example. Amps
can be calculated from watts divided by voltage so in England (and the rest of the UK) a
2000W kettle will use around:
2000W / 230v = 8.7A
In other words around 8.7 coulombs per second. It takes about 90 seconds to boil enough
water for a cup of tea, and, as stated above, an amp is a coulomb per second, so to boil the
water in the kettle it will need:
90 s x 8.7 A = 783 coulombs
We can now finally work out how many electrons we need to make a cup of tea. The
answer is simply the number of coulombs multiplied by the number of electrons in a
coulomb:
783 x 6.241 x 10
18
= 4.887 x 10
21
electrons
Writing that out fully we get:
4,887,000,000,000,000,000,000 electrons
Why not try working out how long it would take to count that number of electrons at a rate of
one electron a second? (Answer at the bottom of the page.)

In the US the mains voltage is lower at 120v. That means even more electrons are needed
to boil the same amount of water. Carrying out the mathematics (as above) it takes about
16.7 amps, or about 9.380 x 10
21
electrons. Note that same amount of power is used in
both the UK and US examples. The difference is that the number of electrons passing a
single point in the wire is greater in the US than the UK, but the energy each electron
possesses is lower. We can either use a lot of low energy electrons, or fewer electrons but
each with higher energy.
Finally, note that the actual number of electrons will be a little different (by percentage) to
those calculated here. For a more precise answer we would need to measure the initial
temperature of the water and take electrical resistance into account, as well as a number of
other factors. Still, the final answer will be close enough and certainly gives a sense of
understanding electric current and its SI unit, the ampere.
Answer to question:
A year is about 60 x 60 x 24 x 365 = 31500000 seconds.
So it would take 4887000000000000000000 divided by 31500000 = 1500000000000000
years to count the electrons at one a second, 24 hours a day, 365 days a year (you can
take a day off each leap year...)
To put this into context, it would take about 1.5 x 10
15
years to count the electrons. The age
of the Universe is about 13.8 x 10
9
years, so it would take longer to count the electrons
than the Universe has so far been around for. Best get started...


Advertisement
Electric current







Electric current is a flow of electricity through a medium and its
SI unit is the ampere, with the symbol A. The flow is typically
through a wire and composed of electrons, the tiny particles that
make up electricity. For most practical purposes the ampere is a
measure of the amount of electric charge passing a particular
point in a given time. To illustrate the ampere we can ask the
simple question: how many electrons does it take to make a cup
of tea?

How many electrons are needed to make a cup of tea?

The next SI Unit is the metre (m). Find out how long it would
take to walk around planet Earth. Other SI units are available
from the menus at the top of the page.


We more often than not refer to amperes simply as amps, and
one amp has the units of 1 coulomb per second. Mathematically
we can show this as 1 A = 1 C/s. But what is a coulomb? It is the
derived SI unit of electric charge and 1 coulomb contains around
6.241 x 10
18
electrons. Let's look at that number written out fully:
624,100,000,000,000,000
Remember that this is the amount of electrons passing a single
point in a wire every single second. There are so many of them
that it's natural to assume that they are whizzing past at some
tremendous speed, but that's not the case. In fact, they are
moving very slowly - typically only about a metre or two an hour,
but they are very, very small.
So we know that 1 A = 1 C/s and we know how many electrons
there are in a coulomb. A typical kettle will draw about 2000
watts of power, and how many coulombs per second that is
depends on the voltage being used. In England, a country
associated with drinking copious amounts of tea, the mains
voltage is 230v so we will use that as our example. Amps can be
calculated from watts divided by voltage so in England (and the
rest of the UK) a 2000W kettle will use around:
2000W / 230v = 8.7A
In other words around 8.7 coulombs per second. It takes about
90 seconds to boil enough water for a cup of tea, and, as stated
above, an amp is a coulomb per second, so to boil the water in
the kettle it will need:
90 s x 8.7 A = 783 coulombs
We can now finally work out how many electrons we need to
make a cup of tea. The answer is simply the number of
coulombs multiplied by the number of electrons in a coulomb:
783 x 6.241 x 10
18
= 4.887 x 10
21
electrons
Writing that out fully we get:
4,887,000,000,000,000,000,000 electrons
Why not try working out how long it would take to count that
number of electrons at a rate of one electron a second? (Answer
at the bottom of the page.)

In the US the mains voltage is lower at 120v. That means even
more electrons are needed to boil the same amount of water.
Carrying out the mathematics (as above) it takes about 16.7
amps, or about 9.380 x 10
21
electrons. Note that same amount
of power is used in both the UK and US examples. The
difference is that the number of electrons passing a single point
in the wire is greater in the US than the UK, but the energy each
electron possesses is lower. We can either use a lot of low
energy electrons, or fewer electrons but each with higher
energy.
Finally, note that the actual number of electrons will be a little
different (by percentage) to those calculated here. For a more
precise answer we would need to measure the initial
temperature of the water and take electrical resistance into
account, as well as a number of other factors. Still, the final
answer will be close enough and certainly gives a sense of
understanding electric current and its SI unit, the ampere.
Answer to question:
A year is about 60 x 60 x 24 x 365 = 31500000 seconds.
So it would take 4887000000000000000000 divided by
31500000 = 1500000000000000 years to count the electrons at
one a second, 24 hours a day, 365 days a year (you can take a
day off each leap year...)
To put this into context, it would take about 1.5 x 10
15
years to
count the electrons. The age of the Universe is about 13.8 x 10
9
years, so it would take longer to count the electrons than the
Universe has so far been around for. Best get started...
Advertisement


