Length









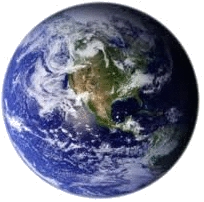
How long would it take to walk around planet Earth? To answer this question we need to
consider distance, or put another way the length of the path we need to take. There have been
many units used for length throughout history and some of them are still in use today, but here
we consider the SI units of the metre, with the symbol m.
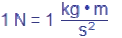

How long would it take to walk around the Earth?
The next SI Unit is the candela (cd). Find out how much brighter a flashlight is than a candle.
Other SI units are available from the menus at the top of the page.


Firstly, a quick comment on the unit name. Strictly speaking it is spelled metre, but in some
English speaking countries meter is used instead. Now, on with the question...
One of the earliest known units of length was the cubit. This was defined as the length of the
arm from the elbow to the tip of the finger. This was further split into smaller units and even
today we still use the "hand" to measure the height of horses. The obvious problem with the
cubit is that it varies depending on the size of the person making the measurement. Other units
where also based on arbitrary measurements with a notable example being the yard, which
although uncertain in origin is often said to be the result of King Henry I (1068 - 1135)
decreeing that it was the distance from the tip of his nose to the end of his outstretched thumb.
What's perhaps surprising is that the SI unit of the metre was also initially based on an arbitrary
measurement, namely the circumference of the Earth.
In 1791 the French Academy of Sciences decided to adopt a new unit of measurement, called
the metre, based on 1/10,000,000th of the distance from Earth's equator to the North Pole.
This was certainly a step forward from nose-to-thumb length, but it also had its problems, such
as the fact that the Earth constantly changes shape a little due to gravitational forces and other
factors. For this reason the metre was slightly changed in length and based on something
much more stable. It is now defined as "the length of the path travelled by light in a vacuum
during a time interval of 1/299,792,458th of a second". Not quite as easy to define as the cubit,
but a lot more precise.
The metre, then, is the SI unit of measurement. It is further split into 100 centimetres (cm), or
1000 millimetres (mm). For long distances it often makes sense to talk in thousands of metres.
One thousand metres is one kilometre, with the units km. For comparison, 1 metre is close to
3.28 feet (about a yard) and 1 kilometre is about 0.62 miles.

King Henry I of England (1068 - 1135) – Often said to be
the originator of the yard.
Now back to our original question of how long it would take to walk around the Earth. At its
equator the Earth's circumference is 40,075 km (24,901 miles). The average walking speed,
depending on age, is about 5 kilometres per hour (km/h), so in 12 hours a distance of 5 km/h
x 12 hours = 60 km is covered. The other 12 hours can be used for sleep and so on.
So to work out how long it would take to walk around the Earth at 5 km/h (about 3 miles per
hour) for 12 hours a day we simply divide the Earth's circumference by the distance walked
in a day:
40,075 km / 60 km = 668 days
This is about 1 year and 10 months. But what if we could drive around the Earth at 100 km/h
(about 60 miles per hour)? Now we cover 100 km/h x 12 hours = 1200 km in a day, so:
40,075 km / 1200 km = 33.4 days
In other words, even if a car is used it would still take about a month to travel all of the way
around the Earth. With the Internet and other forms of global communication, as well as fast jet
transport, we tend to think of the world as quite a small place, but when we think about walking
or driving around it we soon realize that it's actually quite big.
Finally, for most of human history we have thought of distance as being absolute - one mile is
one mile and one metre is one metre. Einstein, in his theory of relativity, demonstrated that in
reality distances shrink when we move at very high speeds. If we travel at about 90% of the
speed of light, distances, in other words lengths, shrink by about 50%. You can read more
about this, together with worked examples, by clicking here.

Click for metres to feet, km to miles and metres to miles converters.
Advertisement


Advertisement
Length








How long would it take to walk around planet Earth? To answer
this question we need to consider distance, or put another way
the length of the path we need to take. There have been many
units used for length throughout history and some of them are still
in use today, but here we consider the SI units of the metre, with
the symbol m.

How long would it take to walk around the Earth?
The next SI Unit is the candela (cd). Find out how much brighter
a flashlight is than a candle. Other SI units are available from the
menus at the top of the page.


Firstly, a quick comment on the unit name. Strictly speaking it is
spelled metre, but in some English speaking countries meter is
used instead. Now, on with the question...
One of the earliest known units of length was the cubit. This was
defined as the length of the arm from the elbow to the tip of the
finger. This was further split into smaller units and even today we
still use the "hand" to measure the height of horses. The obvious
problem with the cubit is that it varies depending on the size of
the person making the measurement. Other units where also
based on arbitrary measurements with a notable example being
the yard, which although uncertain in origin is often said to be the
result of King Henry I (1068 - 1135) decreeing that it was the
distance from the tip of his nose to the end of his outstretched
thumb.
What's perhaps surprising is that the SI unit of the metre was
also initially based on an arbitrary measurement, namely the
circumference of the Earth.
In 1791 the French Academy of Sciences decided to adopt a
new unit of measurement, called the metre, based on
1/10,000,000th of the distance from Earth's equator to the North
Pole. This was certainly a step forward from nose-to-thumb
length, but it also had its problems, such as the fact that the
Earth constantly changes shape a little due to gravitational forces
and other factors. For this reason the metre was slightly changed
in length and based on something much more stable. It is now
defined as "the length of the path travelled by light in a vacuum
during a time interval of 1/299,792,458th of a second". Not quite
as easy to define as the cubit, but a lot more precise.
The metre, then, is the SI unit of measurement. It is further split
into 100 centimetres (cm), or 1000 millimetres (mm). For long
distances it often makes sense to talk in thousands of metres.
One thousand metres is one kilometre, with the units km. For
comparison, 1 metre is close to 3.28 feet (about a yard) and 1
kilometre is about 0.62 miles.

King Henry I of England (1068 - 1135) – Often said to be
the originator of the yard.
Now back to our original question of how long it would take to
walk around the Earth. At its equator the Earth's circumference is
40,075 km (24,901 miles). The average walking speed,
depending on age, is about 5 kilometres per hour (km/h), so in
12 hours a distance of 5 km/h x 12 hours = 60 km is covered.
The other 12 hours can be used for sleep and so on.
So to work out how long it would take to walk around the Earth at
5 km/h (about 3 miles per hour) for 12 hours a day we simply
divide the Earth's circumference by the distance walked in a day:
40,075 km / 60 km = 668 days
This is about 1 year and 10 months. But what if we could drive
around the Earth at 100 km/h (about 60 miles per hour)? Now we
cover 100 km/h x 12 hours = 1200 km in a day, so:
40,075 km / 1200 km = 33.4 days
In other words, even if a car is used it would still take about a
month to travel all of the way around the Earth. With the Internet
and other forms of global communication, as well as fast jet
transport, we tend to think of the world as quite a small place, but
when we think about walking or driving around it we soon realize
that it's actually quite big.
Finally, for most of human history we have thought of distance as
being absolute - one mile is one mile and one metre is one
metre. Einstein, in his theory of relativity, demonstrated that in
reality distances shrink when we move at very high speeds. If we
travel at about 90% of the speed of light, distances, in other
words lengths, shrink by about 50%. You can read more about
this, together with worked examples, by clicking here.


Advertisement